 |
Validierung der hydrologischen Modellierung in DANUBIA
1. Einleitung
Die möglichst korrekte Modellierung des Wasserkreislaufs
und der damit verbundenen Wasserflüsse
zwischen den unterschiedlichen hydrologischen
Komponenten des Einzugsgebiets der
Oberen Donau ist eine zentrale Voraussetzung
für Prognosen zu den zukünftigen Veränderungen
des Wasserhaushalts und deren vielfältigen,
sich daraus ergebenden Folgen. Das verwendete
hydrologische Modell muss die Voraussetzung
erfüllen, dass es prognosefähig ist, d.h., dass es
in der Lage ist, die Wasserflüsse im betrachteten
Einzugsgebiet auch unter zukünftig möglicherweise
stark veränderten Randbedingungen richtig
wiederzugeben. Die Veränderungen der Randbedingungen
beziehen sich auf eine breite Palette
von Faktoren, zu denen u.a. die Folgenden
gehören:
- die Veränderung des Klimas,
- die Veränderung der Landnutzung und der
Landbedeckung (hierin ist die Reaktion der
Vegetation auf verstärkten Wasserstress und
die Änderung der CO²-Konzentration sowie
die Intensivierung der Landwirtschaft eingeschlossen),
- die Veränderung des Gewässernetzes durch
den Einbau neuer wasserbaulicher Strukturen
(Speicherseen, Überleitungen, etc.) und
- die Veränderung der Wassernutzung, z.B.
durch die Einführung vonBewässerung.
2. Das hydrologische Modell PROMET als Ergänzung
zu DANUBIA
Bei der Entwicklung derjenigen Komponenten
von DANUBIA, die die hydrologischen Landoberflächenprozesse
beschreiben, wurde streng darauf
geachtet, die gegenseitigen Wechselwirkungen
durch die entsprechenden Schnittstellen zu
realisieren. Dies führte zu den DANUBIA-Komponenten Surface Soil Biological und Snow & Ice. Sie bilden mit insgesamt über 100 Schnittstellen, über die Variablenwerte ausgetauscht werden,
ein sehr umfangreiches Modellsystem, das die
Komplexität der Landoberflächenprozesse widerspiegelt.
Diese Komplexität der Struktur hat
entsprechende Auswirkungen auf die Performanz
der Komponente Landsurface. Aus diesem
Grund wurde beschlossen, das außerhalb des
Projektes entwickelte hydrologische Landoberflächenmodell
PROMET (Mauser & Schädlich,
1998; Mauser & Bach, 2009) mit DANUBIA zu
verbinden, um für die praktische Umsetzung von
DANUBIA die Performanz zu steigern. PROMET
ist in der Beschreibung der hydrologischen Landoberflächenprozesse
weitgehend identisch mit
den ursprünglichen Landsurface Komponenten,
vermeidet aber die hohe Komplexität der Schnittstellen
dadurch, dass die Komponenten intern
verbunden sind. In DANUBIA wie auch in PROMET wurden
folgende Prinzipien umgesetzt:
- eine vollständig physikalische und physiologische
Beschreibung der Prozesse im Rahmen
der Wasserflüsse in einem mesoskaligen Gebirgseinzugsgebiet.
Folgende Prozesse sind
abgedeckt:
- meteorologische Antriebe entweder von
regionalen Klimamodellen oder von Stationsdaten,
-
Energie- und Masseaustausch zwischen
Landoberfläche und Atmosphäre unter
Einschluss der physiologischen Kontrolle
des Gasaustausches (Interzeption, Evapotranspiration,
sensibler Wärmestrom, Kohlenstoffaustausch,
Strahlungsbilanz, Impulsaustausch),
-
Schnee- und Eisdynamik,
-
Vertikaler und lateraler sowie gesättigter
und ungesättigter Wasserfluss (Infiltration,
Interflow, Oberflächenabfluss, Grundwasserfluss),
- Gerinneabfluss und Fluss durch natürliche
Seen als ein selbstorganisierter, reliefbedingter
Vorgang und
-
Flüsse durch wasserbauliche Strukturen
wie Laufkraftwerke, Speicherseen undÜberleitungen.
- eine strikte Einhaltung der Erhaltungssätze
(Masse und Energie),
- räumlich verteilte Modellierung der Prozesse
auf Grundlage eines isotropen Rasters und
- Erhaltung der physikalischen Konsistenz und
der Prognosefähigkeit durch weitgehenden
Verzicht auf Kalibrierung. Das heißt, dass die
Werte von Modellparametern nicht unter Nutzung
gemessener Abflüsse an Pegeln durch
Optimierung bestimmt werden. Vielmehr werden
Literaturwerte, Messungen (im Gelände
oder über Fernerkundung) sowie die detaillierte
Analyse des Reliefs genutzt, um die Modellparameter
zu initialisieren. Wichtig ist hierbei,
dass alle Verfahren zur Bestimmung der
Parameterwerte für das gesamte Gebiet in
gleicherWeise angewendet werden und keine
teileinzugsspezifischen Regeln und Verfahren
benutzt werden. Damit wird sichergestellt,
dass die Verfahren zur Parameterbestimmung
einen weitenWertebereich abdecken.
Die hydrologische Modellierung wird wegen der
auftretenden Performanzprobleme der Landsurface Komponente in DANUBIA für längere
Modellläufe ab etwa 10 Jahren von PROMET übernommen. Das Zusammenwirken der unterschiedlichen
Wasserkreislauf-Komponenten in
PROMET ist in Mauser & Bach (2009) in seiner
aktuellen Version detailliert beschrieben und in
Abbildung E4.1 in seinem Zusammenwirken mit
DANUBIA dargestellt.
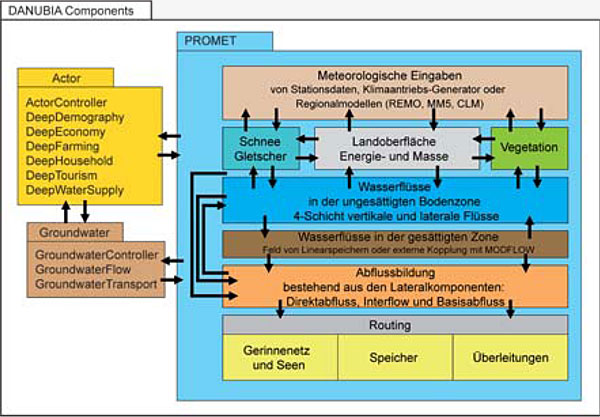 ' '
Abbildung E4.1: Vernetzung der Teilkomponenten des
hydrologischen
Modells PROMET (nach Mauser & Bach,
2009) mit DANUBIA
3. Modellvalidierung
Mit PROMET wurden ohne Kalibrierung für das
gesamte Einzugsgebiet der Oberen Donau die
Wasserflüsse für den meteorologischen Zeitraum
von 1970 bis 2003 modelliert. Diese Untersuchungsperiode
ist länger als die übliche Klimaperiode
von 1971 bis 2000. Zum einen ermöglicht
der Vorlauf von einem Jahr zur üblichen Klimaperiode,
dass sich die Bodenspeicher einpendeln,
zum anderen war beabsichtigt, das ungewöhnlich
warme Jahr 2003 in die Analysen mit
aufzunehmen. Die Modellierung des gesamten
Zeitraums fand kontinuierlich und mit einem Modellzeitschritt
von einer Stunde statt. Die Analyse
der Ergebnisse erfolgte anhand gemessener
Abflüsse an ausgewählten Pegeln im Einzugsgebiet
der Oberen Donau. Diese umfassen sowohl
den Auslass am Pegel Achleiten bei Passau als
auch Teileinzugsgebiete, die so ausgesucht wurden,
dass sie eine breite Palette an Einzugsgebietsgrößen
und hydrologischen Regimes abdecken.
Die ausgewählten Pegel und ihre Einzugsgebiete
sind inTabelle E4.1 aufgelistet.
| Pegel /
Fluss |
Fläche
[km²] |
Höhengradient |
MQ
[m³/sec] |
Abflusskoeffizient |
| Achleiten/Donau |
76.673 |
2,96 |
1590 |
0,55 |
| Hofkirchen/Donau |
46.496 |
2,09 |
640 |
,057 |
| Dillingen/Donau |
11.350 |
1,67 |
162 |
0,57 |
| Oberaudorf/Inn |
9.715 |
4,07 |
307 |
0,78 |
| Plattling/Isar |
8.435 |
2,34 |
175 |
0,58 |
| Laufen/Salzach |
6.112 |
3,46 |
2398 |
0,80 |
| Heitzenhofen/Naab |
5.431 |
1,48 |
49,8 |
0,40 |
| Weilheim/Ammer |
607 |
1,63 |
15,4 |
0,74 |
Tabelle E4.1: Ausgewählte Pegel zur Validierung von
PROMET im Zeitraum 1971-2003. Der Höhengradient ist
hier definiert als das Verhältnis
zwischen durchschnittlicher
Höhe des Einzugsgebiets und der Höhenlage des
betrachteten Pegels. Der Abflusskoeffizient gibt das Verhältnis
des
Jahresabflusses zum Jahresniederschlag an.
Die Tabelle E4.1 zeigt die große Spannweite der
gewählten Teileinzugsgebiete. Sie unterscheiden
sich z.T. erheblich im Höhengradienten und im Abflusskoeffizienten vom Pegel Achleiten am
Auslass der Oberen Donau, welcher das gesamte
Einzugsgebiet repräsentiert. Der modellierte
Bereich der Zentralalpen entwässert hauptsächlich
über Inn und Salzach. Die entsprechenden
Pegel in Oberaudorf und Laufen weisen hohe
Werte des Abflusskoeffizienten und des Höhengradienten
auf. Teile des nördlichen Alpenvorlandes
entwässern über Isar undAmmer/Amper, ihre
Pegel Plattling undWeilheim zeigen mittlere Werte
des Abflusskoeffizienten und des Höhengradienten.
Die niedrigstenWerte finden sich im Teileinzugsgebiet
der Naab im Nordteil der Oberen
Donau.
Die Validierung des hydrologischen Modells fand
in drei Schritten statt: zunächst wurde die jährliche
Wasserbilanz für das gesamte Einzugsgebiet
und die Teileinzugsgebiete bestimmt. Die Ergebnisse
dieser Analyse geben Aufschluss über
die Validität der Flächenmodellierung der Wasserbilanzen.
Sie können wegen des hohen Grades
an zeitlicher Aggregation nichts über die Validität
der lateralen Flussmodellierung aussagen.
Ergänzend dazu ist in Tabelle E4.2 das Ergebnis
einer Regressionsanalyse (Steigung S, Bestimmtheitsmaß
R²) dargestellt. Die Regressionsgerade
wurde so gewählt, dass sie durch
den Nullpunkt führt. Dies ergibt das strengstmögliche
Kriterium für den Vergleich zwischen
Messung und Modellierung, da damit angenommen
wird, dass die Modellierung bei einem gemessenen
Abfluss von Null m³/s ebenfalls Null
m³/s ergibt und damit kein Offset existiert. Hat die
Steigung der Geraden S einen Wert von 1,0, so
besteht keine systematische Unter- bzw. Überschätzung
des Abflusses durch das Modell. Läge
der Wert des Bestimmtheitsmaßes R² gleichzeitig
noch bei 1,0 so wären der gemessene und
modellierte Datensatz identisch.
| Pegel |
Steigung S |
Bestimmtheitsmaß R² |
| Achleiten |
1,05 |
0,93
|
| Hofkirchen |
1,12 |
0,93 |
| Dillingen |
1,14 |
0,93 |
| Oberaudorf |
0,99 |
0,80 |
| Plattling |
1,03 |
0,88 |
| Laufen |
0,93 |
0,85 |
| Heitzenhofen |
1,01 |
0,86 |
| Weilheim |
1,09 |
0,88 |
Tabelle E4.2: Steigung S und Bestimmtheitsmaß R² der
linearen Regression zwischen dem modellierten und gemessen
jährlichen
Abfluss an den ausgewählten Pegeln
im Einzugsgebiet der Oberen Donau; Zeitraum 1971-2003.
Die Steigungen liegen in der Regel nahe bei
einem Wert von 1,0, wobei die höchste positive
Abweichung von 14% Überschätzung am Pegel
Dillingen auftritt und die stärkste Unterschätzung
mit 7% an der Salzach zu finden ist. Die jeweiligen
Bestimmtheitsmaße sind durchweg hoch bis
sehr hoch, was zu der Schlussfolgerung führt,
dass sowohl in den Teilräumen als auch im Gesamtgebiet
die gesamte Variabilität des Abflusses
durch die Modellierung gut erfasst wird.
Als zweiter Schritt wurden die stündlich berechneten
Abflüsse auf Tageswerte aggregiert und
diese mit den an den Pegeln gemessen Daten
verglichen. Die Aggregierung ist notwendig, da
sich sonst größere Unstimmigkeiten im Vergleich
der gemessenen und modellierten Abflüsse ergeben
würden. Sie werden dadurch hervorgerufen,
dass die zeitliche Zuordnung der stündlichen
Niederschläge innerhalb der „Mannheimer
Stunden“ – Zeitintervalle (zwischen 7:30, 14:30
und 21:30 Uhr) im Gegensatz zur stündlichen Abflussmessung - nicht eindeutig ist und damit
nicht-definierte zeitliche Verschiebungen der modellierten
stündlichen Abflüsse von im Mittel ca. 5
Stunden entstehen.
Abbildung E4.2 zeigt den Verlauf der gemessenen
und modellierten täglichen Abflüsse am Pegel
Achleiten für die Jahre 1971-2003. Hier wird
veranschaulicht, dass die gemessenen und modellierten
Verläufe generell sehr ähnliche Niedrigund
Hochwasserabflüsse aufweisen. Relativ
feuchten Perioden um 1980 stehen trockene Perioden,
z.B. der Jahre 1971 oder 2003 gegenüber.
Um die Beziehung der beiden Abflusskurven
in Abbildung E4.2 genauer zu untersuchen,
wurden sie analog zur Vorgehensweise beim jährlichen Abfluss (siehe Tabelle E4.2) einer Regressionsanalyse
unterzogen. Das Ergebnis ist in
Abbildung E4.3 zu sehen. Die modellierten Ergebnisse
zeigen einen leichten Trend zur Überschätzung
der Abflüsse von 3% bei einem sehr
hohen Bestimmtheitsmaß von R²= 0,87. Die extremen
Abflüsse oberhalb von 4000 m³/s zeigen
allerdings eine recht starke Streuung, was darauf
hindeutet, dass die Hochwasserereignisse nicht
mit der für mittlere Abflüsse erzielten Genauigkeit
modelliert werden.
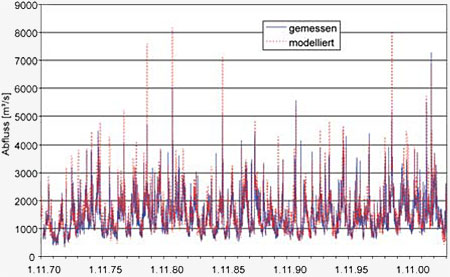
Abbildung E4.2: Gemessene und modellierte tägliche
AbflüsseamPegel Achleiten für die Periode 1971-2003.
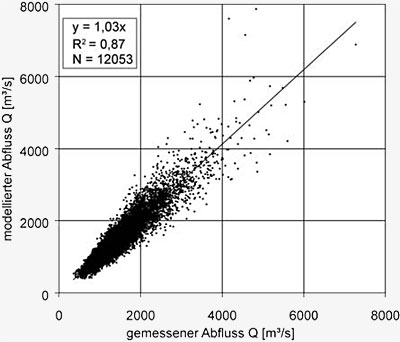
Abbildung E4.3: Vergleich der gemessenen und modellierten
täglichen Abflüsse
am Pegel
Achleiten im Zeitraum
1971-2003.
Das in Abbildung E4.3 dargestellte Vorgehen
wurde für alle ausgewählten Pegel durchgeführt
und führte zu denWerten inTabelle E4.3.Gegenüber Tabelle E4.2, bei der die jährlichen
Abflussvolumina für die unterschiedlichen Pegel
gegenüber gestellt wurden, sind die Unterschiede
in den Steigungen der täglichen Abflüsse ausgeprägter.
Sie reichen von einer mittleren Überschätzung
von 13% in Dillingen bis zu einer mittleren
Unterschätzung der Abflüsse von 14% am
Pegel Laufen/Salzach. Die Bestimmtheitsmaße
der täglichen Abflüsse sind durchweg hoch, aber
geringer als bei den jährlichen Abflüssen (siehe
Tabelle E4.2), was sich aus der größeren Variabilität
der täglichen Abflüsse erklärt. Bei der Betrachtung
des Bestimmtheitsmaßes und des
Nash-Sutcliffe Koeffizienten fällt vor allem der Pegel
Plattling auf. Hier sind beideWerte vergleichsweise
niedrig und es kann in diesem Fall von keinem
guten Modellierungsergebnis gesprochen
werden. Die schlechte Übereinstimmung der gemessenen
und modellierten täglichen Abflüsse
erklärt sich an diesem Pegel vor allem durch den
Einfluss des Sylvensteinspeichers und durch diverse Überleitungen u.a. in das Inn-Gebiet. Der
Sylvensteinspeicher ist zwar im Modell implementiert,
wird aber nach einfachen, normierten
Regeln betrieben, die monatlich die aktuelle
Wasserabgabe mit dem Füllstand regeln (siehe auch Kapitel 2.7.1). Diese einfachen Regeln unterscheiden
sich teilweise deutlich vom tatsächlichen
Betrieb des Sylvensteinspeichers, der aus
externer Sicht nur schwer nachzuvollziehen ist.
An dieser Stelle werden die Grenzen deutlich, die
der physikalisch basierten hydrologischen Modellierung
durch menschliche Eingriffe gesteckt
sind, vor allem wenn die Modellierung Ergebnisse
zu zukünftigen Veränderungen von Abflüssen
aufgrund von Klimaänderungen liefern soll.
| Pegel |
Steigung S |
R² |
Nash-Sutcliffe Koeffizient |
| Achleiten |
1,03 |
0,87 |
0,84 |
| Hofkirchen |
1,11 |
0,87 |
0,81 |
| Dillingen |
1,13 |
0,84 |
0,72 |
| Oberaudorf |
0,94 |
08,1 |
0,80 |
| Plattling |
1,08 |
0,75 |
0,47 |
| Laufen |
0,86 |
0,85 |
0,80 |
| Heitzenhofen |
0,99 |
0,78 |
0,79 |
| Weilheim |
0,98 |
0,73 |
0,69 |
Tabelle E4.3: Steigung S und Bestimmtheitsmaß R² der
linearen Regression sowie Nash-Sutcliffe Koeffizient zwischen
dem modellierten
und
gemessenen täglichen Abfluss
an den ausgewählten Pegeln im Einzugsgebiet der
Oberen Donau; Zeitraum 1971-2003.
Lässt man deshalb das Einzugsgebiet der Isar bis
zum Pegel Plattling bei der weiteren Analyse außer
Betracht, so kann man das Bestimmtheitsmaß
zwischen den modellierten und gemessenen
täglichen Abflüssen in Abhängigkeit von der
Größe des Teileinzugsgebiets untersuchen. Es
ergibt sich dabei eine lineare Beziehung zwischen
Bestimmtheitsmaß und Logarithmus der
Teileinzugsgebietsfläche (siehe Abbildung E4.4).
Die Abnahme des Bestimmtheitsmaßes mit sich
reduzierender Teileinzugsgebietsfläche ist zu erwarten,
da die Anzahl der Proxel und damit die
Anzahl der räumlichen Stützstellen bei der Modellierung
gleichzeitig abnimmt. Aus der Tatsache,
dass die gezeigte Gerade bereits 80% der
Varianz der Daten erklärt, die der Abbildung E4.4
zugrunde liegen, ergibt sich allerdings auch, dass
das Bestimmtheitsmaß offensichtlich nur unwesentlich
von der Lage oder vom Regime des gewähltenTeileinzugsgebietes
abhängt.
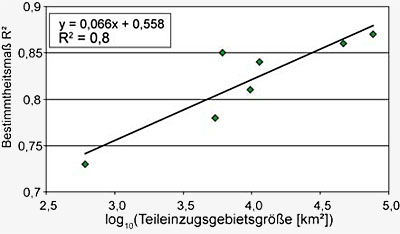
Abbildung E4.4: Abhängigkeit des Bestimmtheitsmaßes
R² von der Fläche der
gewählten Teileinzugsgebiete.
Der
Pegel Plattling wurde wegen der starken anthropogenen Einflüsse nicht berücksichtigt.
Als dritter Validierungsschritt wurden aus den gemessenen
und modellierten jährlichen Abflussmaxima
und -minima am Pegel Achleiten Wiederkehrintervalle
berechnet und verglichen. Die
gemessenen und modellierten höchsten Tagesabflüsse
der Periode 1971-2003 sind in Abbildung
E4.5 dargestellt.
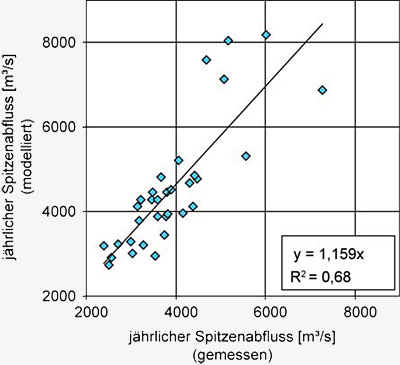
Abbildung E4.5: Vergleich der modellierten und gemessenen
jährlichen
Spitzenabflüsse am
Pegel Achleiten für
die Periode 1971-2003.
sich hier eine systematische Überschätzung der
Spitzenabflüsse um im Mittel etwa 16% bei der
Modellierung. Der Grund dafür ist in der Vernachlässigung
der Ausuferung im Fall größerer Hochwässer
und der damit verbundenen Reduzierung
der Hochwasserscheitelwerte zu suchen.
Diese wird in der Modellierung des Abflusses im
Gerinne zurzeit nicht berücksichtigt. Auch gehen
gezielte Steuerungsmaßnahmen der im Einzugsgebiet
verfügbaren Speicher zum teilweisen
Rückhalt der Hochwasserwelle (z.B. durch Absenkung
der Speicher vor Beginn des Ereignisses)
nicht in die Modellierung der Hochwasserspitzen
ein. Diese können, wie das Beispiel des
Hochwassers in August 2005 gezeigt hat (LfU,
2006), ganz beträchtlich zur Reduzierung der
Scheitelabflüsse beitragen, sind aber zurzeit im
Modell noch nicht implementiert. Abbildung E4.6 zeigt die jährlichen Niedrigwasserabflüsse am
Pegel Achleiten. Hierbei wurde der mittlere 7-tägige
Abfluss (NM7Q) berücksichtigt (siehe auch
Kapitel 3.1.2).
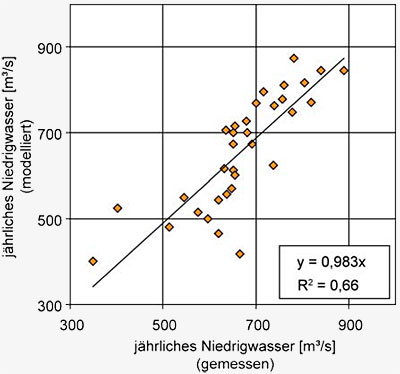
Abbildung E4.6: Vergleich der modellierten und gemessenen
jährlichen
Niedrigwasserabflüsse (NM7Q) am Pegel
Achleiten für die Periode 1971-2003.
Bei den Niedrigwasserabflüssen zeigt sich keine
eindeutige systematische Abweichung zwischen
Messung und Modellierung. Nur zwei Jahre fallen
aus dem ansonsten recht stabilen Trend heraus
und zeigen sehr viel höhere gemessene als modellierte
Niedrigwasserabflüsse.durch Anpassung von Wahrscheinlichkeits-Verteilungsfunktionen
Jährlichkeiten bestimmt. Hierfür
kam im Fall der Hochwasserspitzen die Richtlinie
des DVWK (1999) zur Anwendung. Im Fall
der Niedrigwasserabflüsse wurde angenommen,
dass eine log-Normalverteilung die natürliche
Variabilität des Niedrigwassers im Einzugsgebiet
gut wiedergibt. Die bestimmten Wiederkehrintervalle
für Hoch- und Niedrigwasser sind in Abbildung
E4.7 gegenüber gestellt.
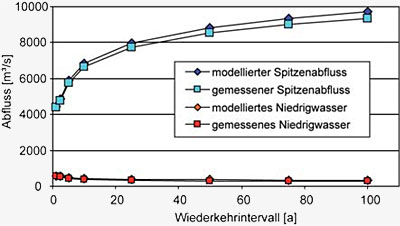
Abbildung E4.7: Vergleich der modellierten und gemessenen
Wiederkehrintervalle für
Hoch- bzw.
Niedrigwasserabflüsse
in Achleiten für die Periode 1971-2003.
4. Zusammenfassung
Die Validierung hat gezeigt, dass der in PROMET
umgesetzte Ansatz die räumliche und zeitliche
Variabilität der Wasserflüsse im Einzugsgebiet
der Oberen Donau mit hoher Genauigkeit wiedergeben
kann. Dies gilt sowohl für die saisonale als
auch für die tägliche Skala und für Teileinzugsgebiete
bis zu einer Fläche von etwa 1000 km². Die
Dynamik der Extreme wird gut wiedergegeben,
wobei eine leichte Tendenz zur Überschätzung
der Hochwasserspitzen besteht. Da keine Kalibrierung
mithilfe gemessener Abflüsse durchgeführt
wurde und weil die Obere Donau ein sehr inhomogenes
Einzugsgebiet darstellt, ist der
Schluss zulässig, dass auch die zukünftigen hydrologischen
Entwicklungen erfolgreich modelliert
werden können.
Autoren
W. Mauser,
Department für Geographie, Lehrstuhl für Geographie und
geographische Fernerkundung, Ludwig-Maximilians-Universität
München
Literatur
Bayerisches Landesamt für Umwelt (Hrsg.) (2006):
Endbericht Hochwasser August 2005, Augsburg, 2006.
Deutscher Verband für Wasserwirtschaft und Kulturbau
e.V. (DVWK) (1999):
DVWK-Merkblatt 251/100, Statistische
Analyse von Hochwasserabflüssen, Bonn.
Mauser, W. & Bach, H. (2009):
PROMET – Large scale
distributed hydrological modelling to study the impact of
climate change on the water flows of mountain watersheds. Journal of Hydrology, 376, pp. 362–377.
Mauser, W. & Schädlich, S. (1998):
Modelling the spatial
distribution of evapotranspiration on different scales using
remote sensing data. J. of Hydrology 212-213, 6 250-267.
 Diese Seite als PDF runterladen. Diese Seite als PDF runterladen.
zurück zur Einleitung-Übersicht

|
 |



